Tendências, sazonalidade e padrões cíclicos.

Séries temporais são observações coletadas ao longo do tempo. É comum aparecer em séries temporais alguns componentes como tendência, sazonalidade ou um comportamento cíclico. Iremos analisar cada um desses componentes, mostrando que é possível decompor uma série em vários componentes e também juntar esses componentes para obtermos, novamente, a série temporal.

Tendência:

Temos uma tendência quando há aumento ou queda de longo prazo nos dados. Não precisa ser linear e pode ocorrer mudanças de tentência nos dados, como sair de uma tendência crescente para uma decrescente.

Sazonalidade:

Existe sazonalidade quando a série é influenciada por fatores sazonais, que podem ser trimestrais, mensais, semanais ou diários. A sazonalidade se apresenta em períodos fixos e conhecidos.

Cíclico:

Padrões cíclicos existem quando os dados apresentam subidas e descidas que não tem períodos fixos. É comum que essas períodos tenham pelo menos dois anos. O que diferencia os padrões cíclicos da sazonalidade é que não apresentam um período fixo e conhecido de flutuações, enquanto as flutuações sazonais acontecem por um período possível de identificar no calendário, além da duração das flutuações cíclicas serem maiores que as sazonais.

Vale destacar que uma série temporal pode ter diferentes combinações desses componentes, ou mesmo apresentar um componente para um tempo gráfico e outros componentes se aumentarmos o período do gráfico.

Decomposição da Série Temporal

Podemos pensar numa série temporal ($y_{t}$) como a junção de três componentes: um sazonal ($S_{t}$), um para tendência-cíclica ($T_{t}$) e um componente para tudo o que resta ($E_{t}$). Representando o modelo de forma aditiva temos:

Ou representando o modelo em sua forma multiplicativa:

O modelo aditivo é mais apropriado quando os componentes não variam com a magnitude dos dados, já quando a variação dos componentes é proporcional à magnitude dos dados os modelos multiplicativos são preferíveis, que é o caso mais comum em economia. Uma alternativa é utlilizar o logarítmo para transformar um modelo multiplicativo em aditivo.

Abaixo o gráfico da série temporal de índice de equipamentos eletrônicos que iremos decompo-las de acordo com seus componentes. Os dados representam a demanda por compenentes elétricos na zona do euro, esta ajustado para dias úteis e normalizado de forma que 100 corresponde a 2005.

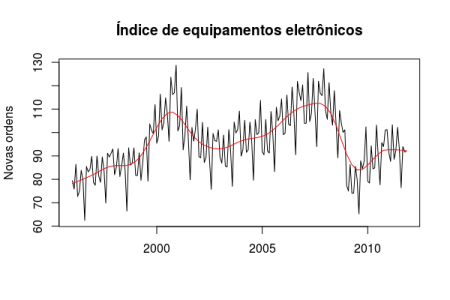
Na cor preta temos a série temporal ($y_{t}$), e foi acrescentado uma linha de tentência vermelha, não estamos destacando sazonalidade e flutuaçoea aleatórias aqui.

Fazendo a decomposição da série podemos representar cada um de seus componentes:

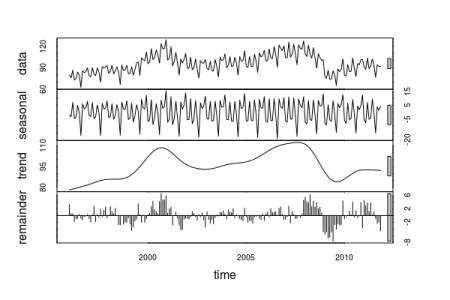
Temos no gráfico a série temporal original, seu componente de sazonalidade, tendência-cíclica e por último, o comportamento aleatório que é tudo que sobra após retirar da série a sazonalidade e tendência-cíclica. Juntando cada um desses componentes temos a série temporal apresentada no início.

Tratamos aqui de padrões e comportamentos mais comuns em séries temporais, uma série pode apresentar uma grande variedade de padrões e é útil poder decompo-la em vários componentes, que representam seus padrões e comportamentos, isso ajuda a melhor entender o que está sendo estudado, com a melhor compreensão, mais chances de conseguirmos uma boa modelagem da série.

Principal Referência:

Hyndman; Athanasopoulos. Forecasting: principles and practice.