Utilizando função auto.arima() no R

Este artigo é motivado por Saz (2011) que analisou a eficácia do modelo SARIMA para a previsão de inflação na Turquia utilizando o algoritmo Hyndman-Khandakar (HK) para derivar o SARIMA. E por Bonno (2014) que compara o modelo SARIMA com um modelo estrutural para previsão de curto prazo de IPCA, encontrando um desempenho superior para o modelo SARIMA no curto prazo.

O modelo SARIMA

É chamado de SARIMA o modelo ARIMA com ajuste sazonal (Seasonal ARIMA). Ok, mas o que é ARIMA? O ARIMA integra dois modelos, um Auto Regressivo de ordem $p$ e um modelo de Média Móvel de ordem $q$, formando uma ARIMA($p,d,q$).

AR($p$)

A parte autoregressiva do modelo faz a previsão utilizando uma combinação linear dos valores passados da variável. O $p$ do AR($p$) indica quantos valores passados o modelo vai utlizar, um AR(2) faz uso de dois valores passados da série.

MA($q$)

O modelo de médias móveis vai uttlizar os erros de previsão passados, de forma que o valor previsto séra uma média móvel ponderada dos erros de previsão passados. O $q$ do MA($q$), assim como no AR($p$), indica quantos lags são utilizados no modelo.

ARIMA($p,d,q$)

No ARIMA($p,d,q$) o $p$ se refere à ordem do AR, o $q$ à ordem da MA e o $d$ diz quantas vezes a série precisou ser diferenciada para ficar estacionária. Em um ARIMA($p,0,q$), o zero mostra que a série já era estacionária e não precisou ser diferenciada, num ARIMA($p,1,q$) a série foi diferenciada uma vez.

ARIMA($p,d,q)(P,D,Q)_{m}$

O SARIMA é representado como um ARIMA($p,d,q)(P,D,Q)_{m}$, em que ($P,D,Q$) representa a parte sazonal do modelo e $m$ reoresenta o número de períodos por sazonalidade.

Para mais detalhes dos modelos uma ótima referência é o livro online do Hyndman e Athana­sopou­los com várias aplicações utilizando o R.

Conjunto de dados utilizado

Para a modelagem utilizaremos a variação percentual mensal do IPCA cheio, que é a série 433 do Banco Central, com início em janeiro de 1980 e término em maio de 2017. Será utilizada a função cpt.meanvar() do pacote changepoint para identificar quebras na série. Segue o primeiro gráfico:

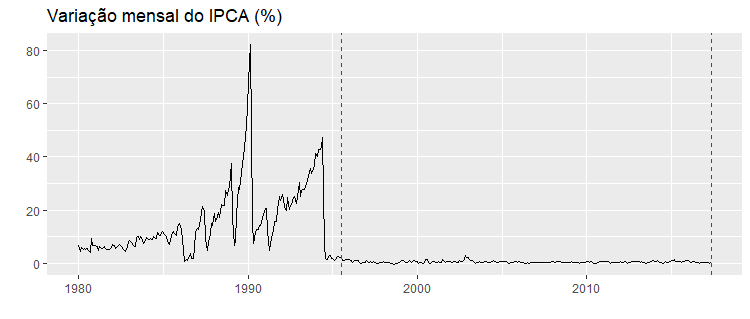
Observe a forte quebra da série em 1994, esse é o nosso sombrio histórico de inflação. Em 1994 o Plano Real consegue por um fim nesse processo inflacionário. Vamos iniciar, então, nossa série em janeiro de 1995, deixando a hiperinflação para trás. Segue o gráfico:

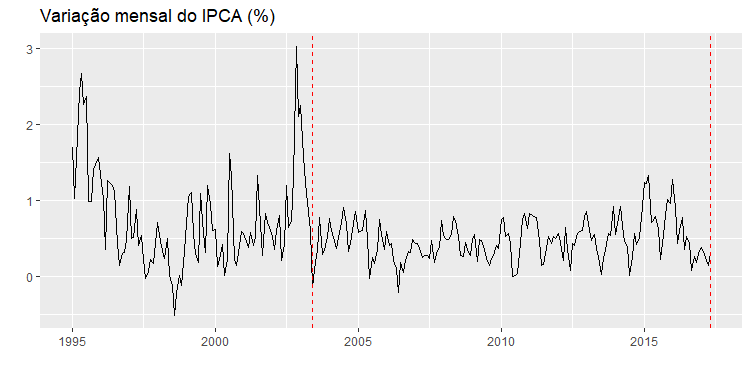
A função cpt.meanvar() aponta uma mudança de média ou variância em junho de 2003. Isso já era esperado por conta do choque inflacionário em 2002/2003, decorrente da candidatura e vitória de Lula para a presidência. Vamos retirar esse período e inciar a série em janeiro de 2004. Segue o gráfico:

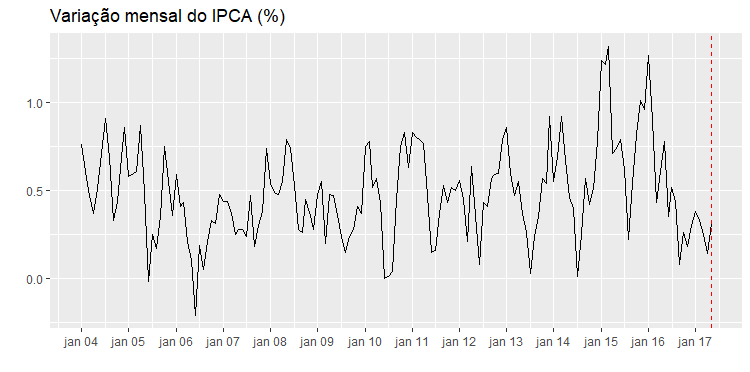
Agora a função cpt.meanvar() não aponta mudanças na série, mas repare na tendência de queda da série em 2005/2006, iremos retirar esse período e iniciar a série em fevereiro de 2007. A série será dividida em duas partes, uma parte que chamaremos de treino, vai de fevereiro de 2007 até maio de 2016 e será utilizada para modelar o SARIMA. A outra parte chamaremos de ** teste**, vai de junho de 2016 até maio de 2017 e será utilizada para avaliar a qualidade do modelo fora da amostra.

A função auto.arima() no R

A função auto.arima() está disponível ao carregar o pacote forecast no R, ela vai escolher as ordens $(p,d,q)(P,D,Q)$ do modelo e compará-las através de um AICc para determinar o melhor modelo. A função emprega uma variação do algoritmo de * Hyndman e Khandakar, que combina testes de raíz unitária, minimiza o *AICc e estima o modelo por máxima verossimilhança (MLE).

Modelo SARIMA, resíduos e acurácia do modelo

Após termos preparado a série e estimado-a com auto.arima(), é possível ver os parâmetros com o comando summary(), que nos apresenta o modelo ARIMA(1,1,1)(0,0,1)[12], ou seja, o modelo vai utilizar 1 lag para a parte autoregressiva e de média móvel, foi diferenciado 1 vez, para os compenentes sazonais 1 lag na média móvel, com uma sazonalidade de 12 meses. O modelo retorna um AICc de -43,54.

Vamos pedir ao R a função de autocorrelação dos resíduos para ver se parece com um ruído branco.

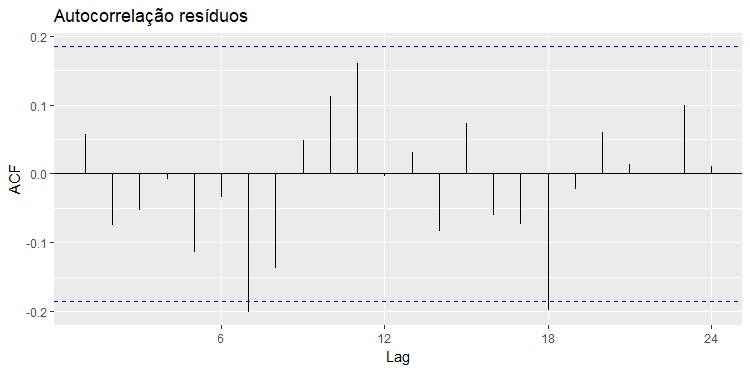
Duas barras passam um pouco do limite pontilhado em azul, ainda assim os resíduos parecem ser um ruído branco. Um teste de Ljung Box ajudará deixar a análise mais objetiva. O teste tem como hipótese nula de que a série a ser testada segue um ruído branco. Nosso teste retornou um P-valor de 0,22, portanto não rejeitamos a hipótese nula e consideramos que os resíduos são ruído branco.

Para testarmos a acurácia vamos utilizar a série “teste” que contém os doze meses de inflação que não foram utlizados para estimar o modelo. É feita uma previsão de 1 passo a frente que é comparada com o valor observado na série teste, isso é feito para o período de junho de 2016 até maio de 2017. Portanto, temos aqui uma avaliação fora da amostra para o período de 12 meses.

A raíz de erro quadrático médio (RMSE) para 1 passo a frente é de 0,12. Quanto maior o período da previsão, pior é a acurácia e maior o RMSE, Uma previsão de 12 meses à frente tem um RMSE de 0,41.

Previsão

Segue um humilde gráfico com a série completa e as previsões:

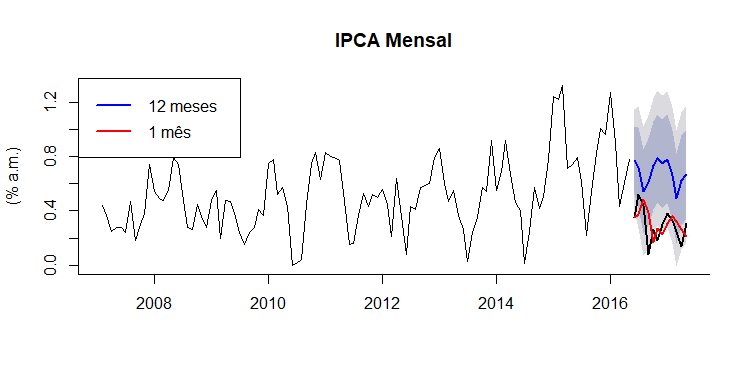
A linha preta em negrito é a série de teste, que não foi utilizada para estimar o modelo e é utilizada para comparar com as previsões. Em azul está a previsão 12 passos à frente, que claramente sobreestima o IPCA. Em vermelho a previsão 1 passo à frente, segue próxima ao valor observado do IPCA, mostrando que o SARIMA é um bom modelo para previsões de curto prazo. Mesmo que seja escolhido algum modelo mais sofisticado para a previsão, é interessante compará-lo com um SARIMA, dados sua simplicidade e facilidade de estimar.

Você pode consultar o código para o SARIMA aqui e os dados aqui.

Referências

BONNO, Simone Jager Patrocinio. Previsão de inflação utilizando modelos de séries temporais. Dissertação de mestrado.

HYNDMAN, Rob J.; ATHANASOPOULOS, George. Forecasting: principles and practice. OTexts, 2014.

SAZ, Gökhan. The efficacy of SARIMA models for forecasting inflation rates in developing countries: the case for Turkey.International Research Journal of Finance and Economics, v. 62, p. 111-142, 2011.